Recently, a La Cañada Math Parent member asked me, “Are there any approaches to teaching math, in the world, that have been shown to be effective?”
My answer is yes, though as you can imagine the question is the source of much debate and subject to many competing answers. There are approaches to teaching mathematics right here in the United States that are extremely effective. After all, the United States has placed first, second or third in 12 of the past 15 years of the International Mathematical Olympiad (IMO) competitions. But this metric reflects what works for the most advanced American students, and one certainty is that the students who compete for the US on its IMO teams, who are mostly of East Asian ancestry anyway, attained their math abilities almost entirely outside of American public K-12 schools (thank you AoPS.) Unfortunately, math achievement results are not nearly as stellar for the average American K-12 student.
At the risk of oversimplification, within the United States there are two major schools of thought on effective math K-12 instruction: the reform math approach that relies on the educational theory of constructivism and which values conceptual understanding over procedural fluency using inquiry learning (a.k.a. discovery learning) and minimally guided instruction, versus traditional math, that relies instead on explicit direct instruction and equally values both procedural fluency and conceptual understanding. These are the same two basic approaches that have been at the center of what is known as the Math Wars, which itself has raged in the United States for well over 40 years. For a primer on the Math Wars, particularly within California, read Professor David Klein’s article “A Quarter Century of US ‘Math Wars’ and Political Partisanship” (2000.)1 While it omits the last 20 or so years, it succinctly describes the two sides, how they evolved, and what political and educational policy battles took place prior to 2000. The Math Wars quieted down on a national level in the 2000s, but flared up again when the Common Core State Standards in Mathematics were developed and adopted by 41 states and the District of Columbia in the 2008 to 2013 time frame, yet 17 states repealed the standards over the ensuing nine years.
The Wikipedia entry on the Math Wars is helpful in understanding the basic positions of the two opposing sides:
https://en.wikipedia.org/wiki/Math_wars
Reform Math: Failing Students for Over 30 Years
Reform math has its roots in the National Council of Teachers of Mathematics (NCTM) 1989 Curriculum and Evaluation Standards for School Mathematics (hidden behind a paywall here but summarized well here), though they were an evolution of the earlier NCTM An Agenda for Action document from 1980. One of the examples of reform math curricula promoted by the National Science Foundation in 1991 to boost the use of the 1989 NCTM Curriculum Standards was Everyday Mathematics, the curriculum developed by the University of Chicago’s School Mathematics Project (UCSMP)2 and adopted by the La Cañada Unified School District (LCUSD) Governing Board for its K-5th grades in 2016. LCUSD still uses Everyday Mathematics to this day. I’ve written extensively on the history behind the contentious selection of Everyday Mathematics in LCUSD on the La Cañada Math website here and how parents adjusted:
https://lcfmathparents.wordpress.com/history/
Everyday Mathematics is a K-6 reform math curriculum widely used across the US that is also widely disliked by students and parents everywhere it is implemented, including in La Cañada elementary schools.3
Key elements of reform math curricula and approaches are:
Emphasis on Conceptual Understanding – Reform math aspires to develop within the novice learner a deep conceptual understanding of mathematical concepts as opposed to rote learning (a.k.a. rote memorization) of math facts and procedures. This is an aspirational goal and those of us who have taught mathematics using both reform math and traditional math approaches and curricula have found no greater conceptual understanding in our students when using reform math approaches. In fact, reform math approaches resulted in more students who not only had no greater conceptual understanding of mathematical concepts, but they could not do basic arithmetic fluently. As the disastrous rollout of the Common Core State Standards in Mathematics (CCSS-M) in the 2010s demonstrated, aspirations do not equate to results. Conceptual understanding today is exemplified by students “explaining their answers,” which more often than not is students parroting teacher-modeled explanations of their notion of conceptual understanding, a phenomenon Katherine Beals and Barry Garelick wryly call rote understanding.4 Another problem with math reformers’ obsession with conceptual understanding is that their description of seeking conceptual understanding over basic skills and procedural fluency is a false choice — traditional math proponents also seek conceptual understanding for their students. For a proper understanding of this false choice, read UC Berkeley mathematics professor Hung-Hsi Wu’s seminal 1999 article, “Basic Skills Versus Conceptual Understanding: A Bogus Dichotomy in Mathematics Education.”5
Must be engaging and personally relevant – Reform math proponents criticize traditional math as boring and lacking relevance to the lives of students. Reformers argue that students must be able to make connections between math concepts and real-life contexts in order to be engaging. And they often gamify instructional activities to elicit greater student engagement. Reviled are math worksheets. Revered are math games and project-based learning based on open-ended prompts. Traditional math supporters respond that traditional math instruction regularly uses real-world problems for practice and to test student knowledge, and the overemphasis on engagement instills within students the false value that all learning must be fun in order to be worthwhile.6
Students must construct knowledge and discover mathematics for themselves – Proponents of reform math rely heavily on the constructivist educational theories of Jerome Bruner7 and Jean Piaget that emphasized student-centered learning and the theory that novice learners must discover or construct some or all of the essential information they are learning for themselves. Reform math theorists and supporters point to educational research that shows that students who discover a fact, rule, principle, or algorithm for themselves are more likely to remember it in the future. While this may be true, they fail to acknowledge the trade-offs of discovery learning — it is less efficient than direct instruction, without timely and proper teacher corrections and feedback it can lead to learning incorrect facts, and random control trials show it is far less effective than direct instruction.8
Group Learning – Reform math supporters champion group work and other forms of collaborative learning. While group learning has its place in the classroom and secondary benefits for children in cultivating group communication and cooperation, studies show it is inefficient compared to direct instruction and poorly designed group work leads to deleterious unintended consequences like social loafing and cheating.
Minimally-Guided Instruction – Because reform math proponents intrinsically believe in the superiority of constructivism and discovery learning, they also believe the fundamental role of the teacher should not be as an expert imparting knowledge to novice students, rather they should facilitate or guide students to construct their own knowledge and understanding. The (nauseating) refrain heard countless times from reform math teachers is, “we are the guide on the side, not the sage on the stage!”
Authentic Problems Only! – Reform math proponents and practitioners loathe math problem worksheets. In fact, they are often derisively called “mindless worksheets.” Students should instead be presented with authentic, culturally relevant, open-ended, real-world problems that require students to think critically and apply what they call “mathematical reasoning.”
De-emphasis of Rote Learning and Memorization – Reform math proponents consider basic calculation skills unimportant and advocate instead the use of calculators and other technology for attaining basic numeracy. Time-honored development of basic mathematical skills like memorizing times tables are considered pointless and antithetical to deeper learning, which is only vaguely defined.
Overemphasis on Calculators and Technology – Since basic skills and mental math are de-emphasized by reform math theorists, they advocate instead the use of calculators and online math tools from a young age — kindergarten in some reform math curricula — not only as a substitute for calculation, but also for exploration and visualization. One of the most inane math activities I’ve seen as a math instructor and parent is an Everyday Mathematics exercise for kindergarteners that attempts to teach the concept of counting integers by entering 1 + 1 on a calculator and repeatedly pressing the = key to see numbers increment on the display.
Teaching of Non-Standard Algorithms – Math reformers hold a special contempt for the standard algorithms of arithmetic. In their 1998 paper “The Harmful Effects of Algorithms in Grades 1-4,”9 educational psychologist Constance Kamii and her co-author Ann Dominick wrote that teaching mathematical algorithms to young children is harmful because it hinders children’s innate mathematical thinking and problem solving abilities. The authors instead advocated that children should be guided to construct their own mathematical principles and thinking. This low quality study, one of the foundational research papers frequently cited by math reformers, was debunked by William Quirk in 2013.10 Regardless, in response reform math proponents encourage the teaching of non-standard algorithms first as if their limited-use algorithms are insulated from the harm they allege results from learning standard algorithms.
De-emphasis of timed assessments – Following the advice of math reform high priestess Jo Boaler, reform math proponents believe timed tests are harmful to students and prefer instead untimed assessments. As Boaler claims on her YouCubed website: “Mathematics facts are important but the memorization of math facts through times table repetition, practice and timed testing is unnecessary and damaging.”11
To understand the problems with reform math approaches, particularly minimally-guided instruction and discovery learning, one should read Kirschner, Sweller and Clark’s seminal paper from 2010, “Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching.":
Summarizing from the abstract:
“Although unguided or minimally guided instructional approaches are very popular and intuitively appealing, these approaches ignore both the structures that constitute human cognitive architecture and evidence from empirical studies over the past half-century that consistently indicate that minimally guided instruction is less effective and less efficient than instructional approaches that place a strong emphasis on guidance of the student learning process. The advantage of guidance begins to recede only when learners have sufficiently high prior knowledge to provide ‘internal’ guidance.”
Traditional Math: The Secret Weapon of Experienced Teachers
Barry Garelick and J.R. Wilson define traditional math in their recent book “Traditional Math: An Effective Strategy that Teachers Feel Guilty Using:”
“Traditional math is the teaching of math using explicit instruction and worked examples to teach a logical sequence of skills and concepts. The method engages students as they develop fact and procedural mastery, algorithms and problem-solving procedures along with reasoning and understanding.”
The key tenets of traditional math are:
Explicit Instruction – Traditional math practitioners prefer explicit direct instruction by expert instructors to novice learners as opposed to the minimally guided or student-led discovery learning methods preferred by reform math advocates.
Mastery of Basic Skills – In the early elementary years, students must learn basic number sense, place value, as well as the fundamental arithmetic operations of addition, subtraction, multiplication and division. Upon these foundational skills, students must learn about fractions and decimals and how to convert between them effortlessly and apply the arithmetic operations to them, measurement, geometry, and data analysis.
Procedural Fluency and Automaticity – Traditional math proponents believe that the memorization of math facts and procedures, which include the standard algorithms, are required to build proficiency and accuracy in mathematical calculations. Another goal of traditional math instructors is automaticity — the ability to perform mathematical computations quickly, accurately, and effortlessly, without the need for conscious thought or extensive cognitive effort, called computational fluency. The related ability to apply well memorized procedures and algorithms smoothly and efficiently to solve novel math problems is called procedural fluency. Computational and procedural fluency, which are often used interchangeably, are seen as the foundation upon which conceptual understanding and problem solving abilities are built. Traditional math practitioners believe practicing math problems is essential to developing understanding, achieving procedural fluency, cultivating accuracy, and extending learning beyond the classroom. Homework that involves practice of skills taught in the classroom, frequently through assignment of problem sets, is regularly assigned in contrast to reform math classrooms, where practice is eschewed as “drill and kill,” and homework minimized or eliminated altogether.
Sequential Progression through Topics – Traditional math proponents emphasize a sequential and linear progression of mathematical topics, where new concepts are built upon previously learned ones in a structured, hierarchical manner. This approach provides a clear and organized framework for students to develop a solid understanding of mathematical concepts.
Focus on Mastery of Standard Algorithms – Traditional math advocates believe the standard algorithms of mathematics such as the long division algorithm should be explicitly taught and practiced to mastery before alternate algorithms are taught. They believe that the standard algorithms provide efficient and reliable methods for solving math problems. UC Berkeley mathematics professor Hung-Hsi Wu explains this and the previous tenet well in his 2009 critique of Everyday Mathematics:12
“Mathematics is simple and clear, and its progression is orderly and hierarchical. We want children to learn the most basic things, and learn them well each time, so that they can move to the next stage with a clear understanding of what they have learned, and what they can do next with their new-found knowledge. Some skills and concepts in elementary mathematics are so important (place value, standard algorithms, etc.) that one must not leave the learning of such things to chance. They must be learned, and learned well, and the only way to do this is to isolate them and give children time to absorb them. When you do the standard algorithms as some items among a few dozen that children should know, you are doing public education a disservice. You are in fact misleading the public by design, because it allows you to claim, on the one hand, that you recognize the importance of these basic skills and concepts and, on the other, pander to the ideology of others by making the learning of said skills and concepts virtually impossible.”
Emphasis on Accuracy – Traditional math proponents value correctness and accuracy in mathematical computations. Attention to precision and correct usage of mathematical language and properties is important in developing strong problem-solving abilities and preparing students for higher-level mathematics.
Problem Solving – Reform math supporters claim that mathematical problem solving is the goal of their reform methods and is ignored in the traditional math classroom. This could not be further from the truth. Traditional math practitioners liberally use real-world word problems in assigned problem sets and on assessments to test students’ ability to apply the math knowledge they have learned. In fact, Singapore Math has a reputation for its fiendishly difficult word problems that stretch the ability of students to apply math facts and procedures learned in the classroom.
Timed Assessments – Traditional math proponents also do not avoid timed assessments as reform math proponents frequently do. In fact, timed assessments are considered critical in the development of mental math and computational fluency in the early elementary grades. This is in recognition of the limitations of human cognitive architecture. In the 1980s, cognitive scientists developed and advanced cognitive load theory, which posits that all novel information first is processed by a capacity and duration limited working memory, and then stored in an unlimited long-term memory for later use.13 Working memory is limited to about half a dozen bits of novel information, while long-term memory is nearly limitless and recall nearly instantaneous. Cognitive load theory recognizes that when working memory becomes overloaded, cognitive performance suffers, which leads to errors and reduced learning efficiency. For this reason, traditional math supporters emphasize memorization of math facts and procedures to commit them to long-term memory, thus freeing up working memory to focus on the more challenging aspects of solving a math problem.
Delayed Use of Calculators – Most traditional math teachers delay introduction of calculators until middle school at the earliest, in contrast to math reformers’ preference to introduce them in the early elementary grades.
The Science of Math is a recent educational movement that started in 2020 and uses an evidence-based approach to K-12 mathematics instruction, incorporating all of the traditional math tenets described above. Its developers followed the success of the Science of Reading approach to early literacy and applied it to early math instruction and math remediation in particular for struggling students. The Science of Math is, in the words of its creators, “focused on using objective evidence about how students learn math in order to make educational decisions and to inform policy and practice.” Its proponents provide resources for teachers that they say follows high quality education and cognitive science research. While the Science of Math movement has only recently started, the resources and material they have produced so far show promise for providing a framework for evaluating the effectiveness and worth of math education theories, approaches, and curricula.
Lessons from Other Higher Performing Countries
As alluded to earlier, while the United States has been successful in producing world-class students of mathematics at the very high end of the math ability curve, the country has miserably failed most of the rest of its students. The recent results of the National Assessment of Educational Progress (NAEP)’s Nations Report Card for 13-year olds shows over 20 years of slow and steady gains in math proficiency were wiped out with lightning rapidity during the nation’s response to the COVID-19 pandemic.14 As for countries that use a traditional math approach that eclipse the US in international benchmarks like the Trends in International Mathematics and Science Study (TIMSS) and the OECD’s Programme for International Student Assessment (PISA), look to East Asian countries, particularly Singapore (#1 in 2019 TIMSS 8th grade math), South Korea (#3), Japan (#4), and Hong Kong (#5):

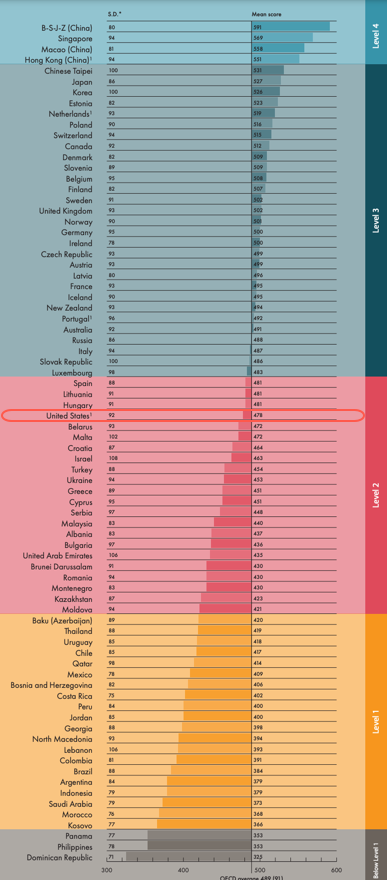
For context, US 8th graders ranked 16th out of 46 participating countries and cities tested as a system. The PISA results are worse for the US, which ranked 37th in the most recent results:
For context, the gap between Singapore and the US is equivalent to three years of math education!
Looking to #1 ranked Singapore for inspiration, the key elements of the Singapore Math approach include:
Concrete-Pictorial-Abstract (CPA) Approach – This instructional method starts with concrete manipulatives to represent mathematical concepts, then progresses to pictorial representations, and finally moves towards abstract representations. It helps students develop a solid foundation by connecting mathematical ideas to real-world experiences.
Problem Solving – Singapore Math places significant emphasis on problem-solving skills. Students are encouraged to solve a variety of mathematical problems, including both routine and non-routine ones. This approach aims to develop critical thinking, logical reasoning, and analytical skills.
Model Drawing – Model drawing is a visualization strategy used in Singapore Math to solve word problems. It involves representing a complex problem situation with a visual model, such as bar diagrams, to help students understand the problem structure and relationships. It supports the translation of word problems into mathematical expressions.
Mastery Approach – Singapore Math focuses on achieving mastery of mathematical concepts before moving on to new topics. It emphasizes a depth-first approach, where students develop a thorough understanding of a topic before progressing to the next one.15
Strangely, given LCUSD adopted the reform math Everyday Mathematics curriculum in 2016 for grades K-5, LCUSD adopted an Americanized version of Singapore Math called Math In Focus: Singapore Math by Marshall Cavendish when it adopted its math curriculum for middle school in 2017. I call the selection of Math In Focus strange because Singapore Math is diametrically opposite Everyday Mathematics in design and approach. The fact these two starkly different curricula are in use is not unusual in another sense because there was a huge battle during the adoption of Everyday Mathematics in 2015 and 2016 in LCUSD as mentioned earlier and explained elsewhere. Parents preferred Singapore Math. The majority of teachers and administration supported the adoption of Everyday Math. Parents lost. But many parents responded by compensating with tutors and seeking supplemental math instruction outside of schools using traditional math curricula and approaches.
There are several other math curricula besides Math In Focus available in the US that use a traditional math approach to mathematics instruction. For example, some private schools, many home schoolers, and I myself used with my kids when they were very young an earlier version of Singapore Math called Singapore Math: Primary Edition, which we believe is superior in many ways to the American Common Core-aligned Math In Focus version of Singapore Math.16 Many older math curricula created years prior to the 1989 NCTM standards and Common Core follow a traditional math approach and are still heavily used by homeschoolers and private and parochial schools. Perhaps most popular among those is Saxon Math, though I have no personal experience teaching it.
One of the limitations of the various flavors of Singapore Math is it stops at Algebra in high school. When a child gets to Algebra I, one needs to switch to a different curriculum. In keeping with the adage that older is better, which holds true in general for mathematics textbooks in the United States, I frequently find myself using a classic Algebra I textbook many of us math instructors call Brown & Dolciani, named after its two principal authors Mary P. Dolciani and Richard G. Brown. Titled “Algebra: Structure & Method,” the textbook was originally written in 1962 and went out of print in 2000:
Caveat: The Teacher Matters More than the Textbook
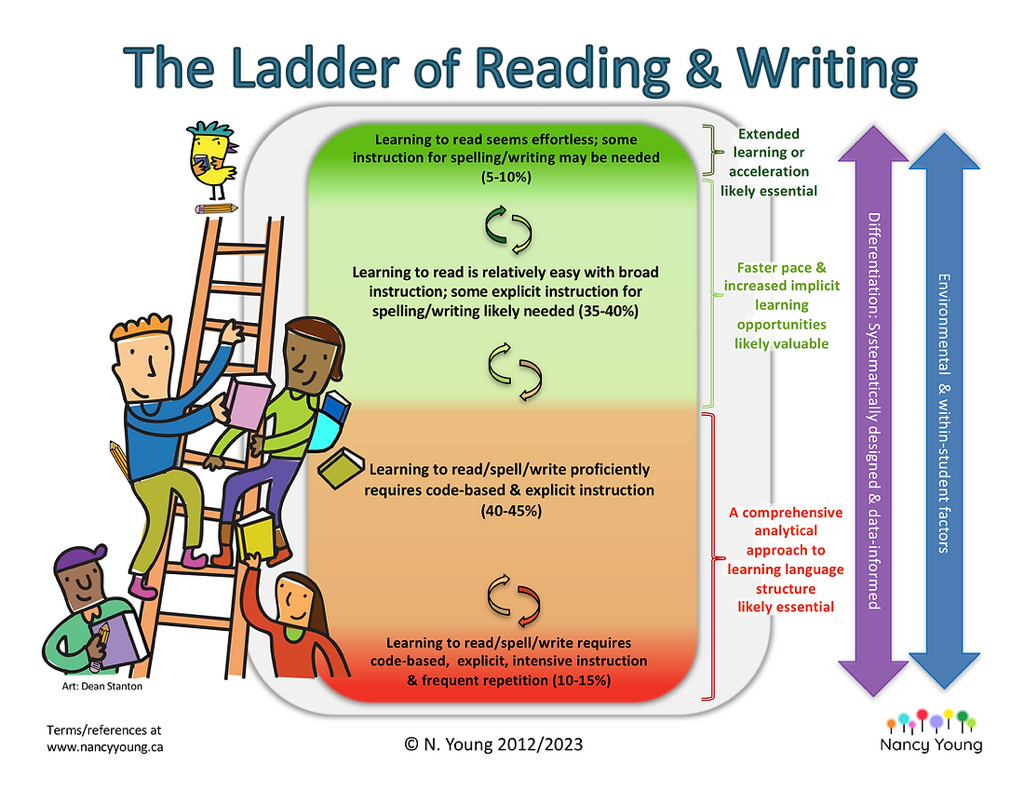
The architects of the Science of Math would do well to learn from the experience of the proponents of the Science of Reading (SOR.) There’s a famous graph in SOR created by Nancy Young called The Ladder of Reading & Writing shown below:
Though I have not found any research that attempts to categorize how easily children learn mathematics, I surmise a distribution similar to Nancy’s Reading & Writing Ladder infographic exists for mathematics instruction. This means for a small percentage of students, learning math is relatively effortless and they can quickly master mathematics concepts regardless of what math curriculum is used, and what teacher teaches it. In fact, the most precocious can learn mathematical concepts independently with a well-written textbook or even without a textbook given a skilled tutor, teacher, instructor, or mentor. However, for the next two cohorts of math learners, explicit instruction is required for learning to be effective. And for the small but still significant percentage of students at the other end of the distribution -- students who struggle with mathematics and who have diagnosed learning disorders like dyscalculia -- explicit instruction is critical to success. Placing such students in a discovery-learning classroom is a mathematical death sentence.
Even with the most effective instructional materials and a focused and motivated student, math instruction can be diminished or even sabotaged by a poor teacher. As an example, many districts that adopted Singapore Math in the early 2000s failed in their implementations because teachers were not properly trained how to teach the material and continued to use constructivist and group-centered teaching methods that they were taught in ed school.17
Several studies of the common ingredients of higher performing East Asian countries in their elementary and pre-college math education find that most, in contrast to the United States, have higher credential requirements for teachers who teach mathematics in the elementary grades. American K-5 teachers only require a general education credential, not a math credential. In contrast, elementary teachers in China, Singapore, and Finland have higher math qualification requirements.
Final Words
This essay began as an attempt to answer a simple question — “are there any approaches to teaching math, in the world, that have been shown to be effective?” A thorough answer would involve a book-length treatment, but I have tried to summarize the salient issues involved in American K-12 mathematics education and wisdom gained from years teaching basic and competition math to elementary through high school students. I write this on a sad day for education in California, and probably the United States more broadly speaking given California’s oversized influence on the textbook publishing market. The California Board of Education voted on this day to approve a new California Mathematics Framework (CMF) for its six million K-12 public school students. The decision ends a four-year battle over the future of California children’s math education. The California Board of Education adopted an equity-focused disaster of a framework that will doom generations of California public school students if parents leave their children’s education to the wisdom of California education bureaucrats and their hired gurus who wrote the CMF document. Reform math in orientation through and through, the CMF’s authors and supporters claim it develops basic math skills and procedural fluency too! I wrote about the problematic first draft of the CMF when it was released in 2021. The third draft that was approved today by the California Board of Education was not much better. This points to a dark future for American pre-college students as far as math education is involved.
Parents should respond as they always have when benighted math education policies are adopted by government education ‘experts’ — take control of your child’s math education. Decide that you will not leave the fate of your child’s math future, and the potential careers it unlocks, to public school administrators and paid math education consultants christened in the cesspool that is American schools of education. Fortunately, the United States remains a pluralistic, relatively free nation with plentiful education options. Seek out alternate educational paths, and if you are stuck in a public school or a progressive private school that uses the latest fashionable math education approach based on the CMF, supplement your child’s classroom math education with outside mathematics through one of the many math enrichment centers, online programs, or private tutors.
David Klein, “A Quarter Century of US ‘math wars’ and Political Partisanship,” BSHM Bulletin: Journal of the British Society for the History of Mathematics, Vol. 22, Issue 1, pp.22-23 (2007.) A copy of the article may be found online on Professor Klein’s professional website. For an excellent article by Professor Klein with a longer scope looking back at US math education over the entire 20th century, see “A Brief History of American K-12 Mathematics Education in the 20th Century,” Mathematical Cognition (2003.)
For more information about Everyday Mathematics see my pages about EM on my La Cañada Math Parents website here: https://lcfmathparents.wordpress.com/about-everyday-math/.
Katherine Beals and Barry Garelick, “Explaining Your Math: Unnecessary at Best, Encumbering at Worst,” The Atlantic, November 11, 2015.
Hung-Hsi Wu, “Basic Skills Versus Conceptual Understanding: A Bogus Dichotomy in Mathematics Education,” American Education, Fall 1999.
For an excellent demolition of the notion that all math learning must be fun and engaging, read this classic refutation by Konstantin Kakaes, “Math Has to be At Least a Little Boring,” in Slate online:
“The Times’ misunderstanding comes from a failure to appreciate that mathematics—even at the basic level taught to elementary, middle, and high school students—is an intellectual discipline with content intrinsic to itself. This content is important and can be made exciting and accessible without reference to the ‘real world.’
Let’s take a simple example: 3 + 5 = 8. It is useful to know this sum without reference to 3 apples and 5 apples, or 3 cars and 5 cars, or 3 computers and 5 computers. It is an abstract fact, just as knowing that 8 x 9 = 72 is an abstract fact. Understanding these abstractions then lets us turn to a multitude of real-world applications. It is the knowledge that 3 of anything and 5 of anything adds up to 8. Thinking about apples may help a young child learn to add in the first place, but it isn’t a substitute for subsequently developing the abstract skill of addition, which requires practice. The Times’ dichotomy between “real-world problem solving” and “traditional drills” does not exist. As in learning foreign languages, repetitive drills enable students to master techniques—of which addition is the simplest example—which can then be used to solve problems in the real world, and to develop more mathematical sophistication, which can then be bolstered by using new mathematical concepts in the real world. This is true in arithmetic, and also in algebra, geometry, calculus.”
Jerome Bruner, (1961). “The art of discovery,” Harvard Educational Review, vol. 31, pp.21–32.
John Sweller, Paul Ayres, and Slava Kalyuga, Cognitive Load Theory, Springer (New York), 2011.
Constance Kamii and Ann Dominick, “The Harmful Effects of Algorithms in Grades 1-4,” in Lorna J. Morrow and Margaret J. Kenney, eds., The Teaching and Learning of Algorithms in School Mathematics, 1998 Yearbook (Reston, VA), National Council of Teachers of Mathematics, 1998), pp. 130-40.
William Quirk, “The Bogus Research in Kamii and Dominick’s Harmful Effects of Algorithms Paper,” Non-Partisan Education Review (2013.)
Jo Boaler and Cathy Williams, “Fluency Without Fear: Research Evidence on the Best Ways to Learn Math Facts,” Jan. 28, 2015. YouCubed.org website.
Hung-Hsi Wu, from the Palo Alto Parents 2009: Math website.
John Sweller, Jeroen J.G. van Merriënboer, “Cognitive Architecture and Instructional Design: 20 Years Later,” Educational Psychology Review, vol. 31 (2019, pp. 261-292. For a (short) book-length treatment on cognitive load theory and its lessons for classroom teachers, read Greg Ashman’s “A Little Guide for Teachers: Cognitive Load Theory.” (2023)
Dana Goldstein, “What the New, Low Test Scores for 13-year Olds Say About US Education Now,” New York Times, June 21, 2023.
As retrieved from ChatGPT 4.0 on July 11, 2023.
Parents and teachers can still buy the Singapore Math: Primary Edition via its US distributor’s website: https://www.singaporemath.com/pages/primary-mathematics-resources







Nicely written and very comprehensive review of the issues with reform math, and a good comparison with traditional math. My co-author and I were interviewed by Anna Stokke on her podcast, focusing on our book, and the issues with math education. https://chalkandtalkpodcast.podbean.com/e/ep-6-math-teaching-tips-with-barry-garelick-and-jr-wilson/